
What is the Decision Rule?

According to ILAC_G8:09/2019, a decision rule is defined as a rule that determines how uncertainty is accounted for when stating conformity with a specified requirement.
Why Is It So Important, Regarding Calibrations and ISO 17025?
The decision rule is an important part of calibrations and ISO 17025 compliance. The ISO/IEC 17025 standard requires labs to have decision rules when making statements of conformity because they define exactly how the lab personnel determine if measurements are intolerance or out of tolerance. Having those definitions is part of why accredited labs are a more reliable outsourcing solution for calibration needs. Another reason is the standard requires that the lab provide evidence for the competence of personnel required to make decisions about conformity. So, accredited labs usually have more detailed training programs for calibration technicians because they’re required to remain ISO 17025 accredited.
Example of a Decision Rule in Practice
Let’s take a simplified example to demonstrate a decision rule and its impact on calibration. In this instance, we’ll statistically analyze (10) 20 µL samples of water dispensed from a pipette. To help streamline the concept, we’ll ignore any environmental conditions and correlation factors.
In this example, we will:
Table 1
| Accuracy Target % | Precision Target % |
| 1.0 | 0.5 |
To take the 10 measurements, the pipette is used to aspirate and dispense the desired volume of liquid from the water sample (as seen in Image 1) then the analytical balance is used to make the measurement. Since the analytical balance measures the mass of the liquid (in this case water), not the volume, the density of the water (0.998 g/ml) will be used to convert the mass measurement units to volume units.
The magnified mass measurement value shown on the balance is the mass equivalent to the volume drawn by the pipette at the 20 µL setting. Using all 10 measurement values from our example, we will determine if the accuracy and the precision of the pipette are in or out of tolerance. The accuracy can be thought of as how close to 20 µL each measurement is; we will use the average of all measurements to check the accuracy. The precision value is how spread apart all the measurements are in relation to one another; we will use the average deviation of the measurements as the precision value in this example.

Image 1
Recall that the upper and lower acceptance limits () for the pipette volume measurements are specified by Standard ISO 8655-2:2022 (E). We are going to have a set of acceptance limits for precision and accuracy values. In our example calibration, we are using the 20 µL pipette setting. The accuracy of the pipette is how close the measurement is to 20 µL and that accuracy target is 1% of 20 µL or 0.2 µL. In Image 2, you can see that the upper and lower acceptance limits for the accuracy are:
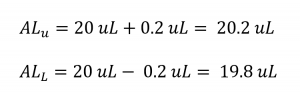
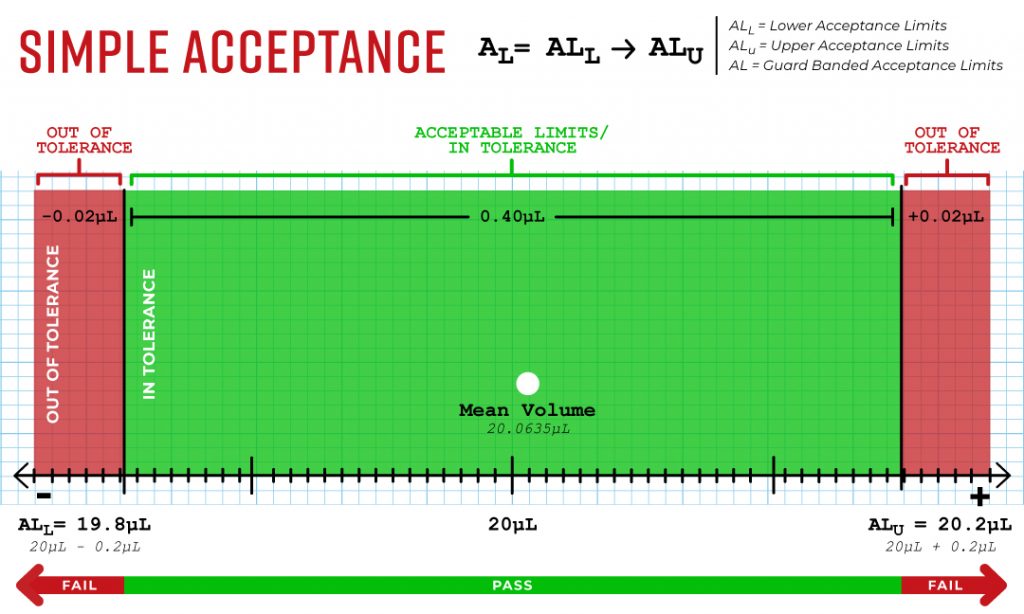
Image 2
These acceptance limits can be used to determine if a pipette is in or out of tolerance. Using a simple acceptance rule, a measurement between 19.8 µL and 20.2 µL would be considered in-tolerance; anything outside those limits would be considered out of tolerance. Notice, in the example, the average of the 10 volume measurements is 20.0627 µL, which is inside our acceptance limits. So, the accuracy of the pipette is intolerance.
The next decision is about the precision of the pipette. Precision is defined as the average deviation of the 10 measurements. The allowed amount of average deviation according to the ISO standard (Table 1) is 0.5%. This percentage is found by dividing the average deviation by the average of the measurements. In our example, average deviation (0.0135 µL)/average (20.063 µL) is equal to 0.067%. This is less than the allowed 0.5%, so this pipette’s precision result is in-tolerance.
Simply using the upper and lower limits to make those decisions, as shown here, is an example of simple acceptance, which is defined later. There are other ways to make decisions about measurements that are more complicated than simple acceptance.
A Deeper Look into the Decision Rule
As stated earlier, the decision rule is a rule that determines how uncertainty is accounted for when stating conformity with a specific requirement. There are many ways of expressing a decision rule. The examples we include here are binary simple acceptance and binary simple acceptance with guard-band considerations, but there are other ways of expressing decision rules.
Simple Acceptance
A binary simple acceptance rule exists when there are two possible outcomes, pass or fail. An example of binary simple acceptance is when the decision rule states that a pass is a measurement result that is within the acceptance limit and a failure is one that is outside the acceptance limit. An example of binary simple acceptance was our example of checking the accuracy and precision of the 20 µL pipette.
Simple Acceptance with Guard-Banding
Guard-banding is a way to incorporate uncertainty in the decision rule and reduce the risks associated with pass and fail assignments that are close to the acceptance limits. The best way to visualize this is to use an example of a binary decision rule with guard bands. The decision to pass is based on whether the measurement is within the acceptance limits (AL) minus a guard band (GB). Thus, GAL (guarded acceptance limits) = AL − GB. The guard-banded range is usually defined using the expanded uncertainty value. The expanded uncertainty range of the pipette can be placed on the upper and lower acceptance limit lines, creating a guarded acceptance zone. We will use an expanded uncertainty of ± 0.028 µL for this 20 µL pipette example. This expanded uncertainty value is just an example; it is not calculated from the example data in our earlier pipette example.
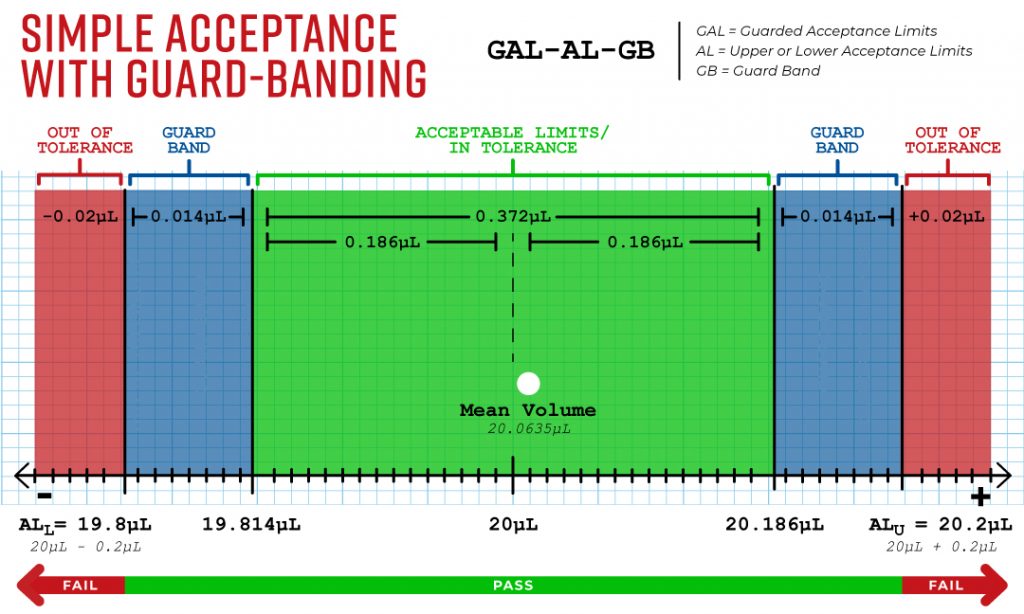
Image 3
As you can see from Image 3, there is a specification acceptance zone (the green plus the blue shaded ranges) and a guard-banded acceptance zone (the strict acceptance zone in green). The blue zone is half of the expanded uncertainty 0.028 µL / 2 = 0.014 µL. So, the strict in-tolerance zone in green is going to have the following acceptance limits:
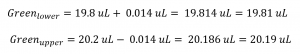
This strict acceptance zone creates a reduced risk acceptance zone. So, anything within the green area would be a pass and anything outside the green area would be a failure (using the binary decision rule stated earlier). Guard-banding is used because it reduces the risk of false acceptance by banding the upper and lower specification limits. You can think of this as a safeguard.
A common question is why do I need guard-banding if I have the specification limits already? The reason is that all measurement values have an uncertainty associated with them. So, if you have a measurement value that comes close to the upper specification limit, there is a possibility that the true value of that measurement is beyond the specification limits. This is how guard-banding reduces the risk of false acceptance and false rejection.
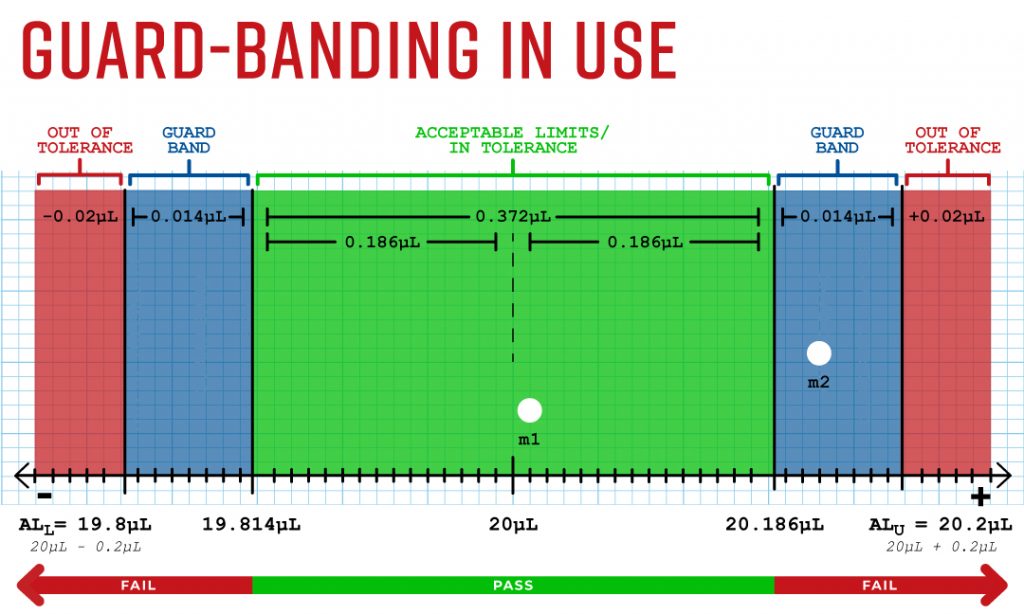
Image 4
Notice in Image 4 the dots representing measurements 1 (m1) and 2 (m2). The use of guard bands shows that m1 would be the only in-tolerance measurement because m2 is not in the strict acceptance zone. It’s worth noting that measurements in between the guard band and the specified limits can be deemed intolerance if certain decision criteria allow for it. This would depend on how the lab, or the customer, chooses to handle those measurement results.
What Does the ISO/IEC 17025 Standard Say About Decision Rules?
The ISO 17025 standard requires the laboratory to have a documented decision rule for making statements of conformity. There are other requirements worth noting here:
So, these ISO/IEC 17025 requirements exist to make sure that accredited laboratories are defining the way they make statements of conformity with decision rules. They are making sure that laboratories are authorizing competent personnel to make decisions about conformity. The standard requires that when customers request information about decision rules and statements of conformity, the calibration laboratory can provide documentation that outlines its processes for making decisions. Basically, ISO/IEC 17025 ensures that accredited laboratories are held accountable for their decision criteria, and this is why outsourcing your calibrations to accredited labs is so important.
Challenges and Solutions
A common challenge related to decision rules is training authorized personnel in the laboratory to make judgments about conformity. Decision rules can be complicated, and making sure that technicians and managers are knowledgeable about the decision rules the lab uses can be a major challenge.
Another challenge is deciding what decision rule is appropriate to use. There are many instances where the customer may not even read the decision rule on your calibration certificate; they are just looking for “pass” or “fail.” If that is the case, then why not use binary simple acceptance without guard-banding for everything? To answer this, we need to think about risk and the probability of false acceptance and/or false rejection. Many times, the customer will know if they need guard-banding rules because they are adhering to government or private regulations. So, they will ask the calibration lab for specific decision criteria.
What Are the Best Practices for Creating Decision Rules?
The answer is that best practices vary depending on the needs of the lab and the customer. For most cases, simple acceptance will suffice, and we see that in practice as simple acceptance is a very common decision rule referenced on calibration certificates. If a customer has a specific need for more stringent acceptance and rejection criteria, such as if they are being regulated by private or governmental standards, simple acceptance may not be the best option. A couple of examples of other decision rules that may need to be used are a binary simple acceptance with a defined guard band and/or a non-binary statement with a defined guard band.
Conclusion
The decision rule that a lab uses to determine if a measurement is intolerance or out of tolerance is important. When calibrating pipettes, it may be acceptable to use a binary simple acceptance rule to make statements of conformity, but understanding the meaning behind that simple acceptance rule will help customers understand their calibrations and why they are so important. Recall that the ISO/IEC 17025 standard requires laboratories to document their decision rules and to train and authorize staff to make decisions about conformity. So, it’s important to use an ISO/IEC 17025 accredited laboratory for pipette calibration because they are best qualified to establish whether your pipettes are in or out of tolerance.
Are you currently using an ISO/IEC 17025 accredited laboratory for your pipette calibrations? If you aren’t or don’t know, reach out for more information about how we can help.
Sources
[1] Accreditation Committee of ILAC (2019) Guidelines on Decision Rules and Statements of Conformity ILAC.
